다익스트라(dijkstra)

다익스트라 알고리즘

다익스트라 알고리즘은 최단 경로(shortest path)를 찾는 알고리즘이다. 최단 경로를 찾는 문제는 보통 각 정점들을 연결하는 경로들의 가중치의 합이 최소가 되는 경로를 찾는 방식으로 구한다. 지하철 노선을 예로 들었을 때, 정점은 역이 되고, 가중치는 역간의 소요시간이 된다. 위처럼 다익스트라 알고리즘은 지하철역의 최단 경로를 구할 때와 같이 일상생활에서 최단 경로를 구할때 자주 사용될 수 있다.

이런 다익스트라 알고리즘을 적용하기 위해서는 그래프(Graph)자료구조로 데이터가 구성되어야 있어야 한다. 그럼 최단 경로를 어떻게 구하는지 알아보자.

아래그림은 총 8개의 정점들이 연결되어있는 그래프 자료구조로 정점 0에서 출발하여, 정점 3까지의 최단경로를 나타내고 있다.

그래프(Graph) 데이터

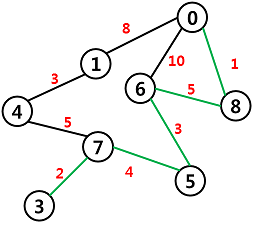
정점 0에서 3까지의 경로를 살펴보면 0-8-6-5-7-3 으로 이어지는 것이 확인된다. 최소경로는 0-6-5-7-3 이 될 수 있지만, 총 거리가 21로 최단경로의 거리인 15보다 크므로 최단거리가 될 수 없다. 즉, 정점간의 weight에 따라 최단 거리는 달라지게 되는 것이다.

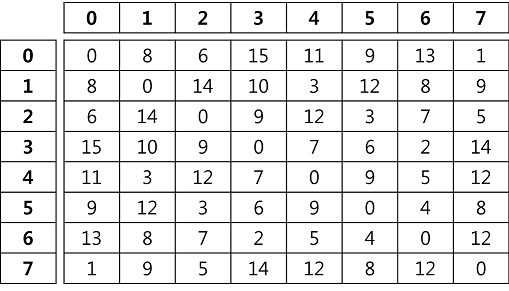
위 그래프의 데이터로 부터 아래그림과 같이 2차원 배열로 Weight 값을 나타낼 수 있다. Weight

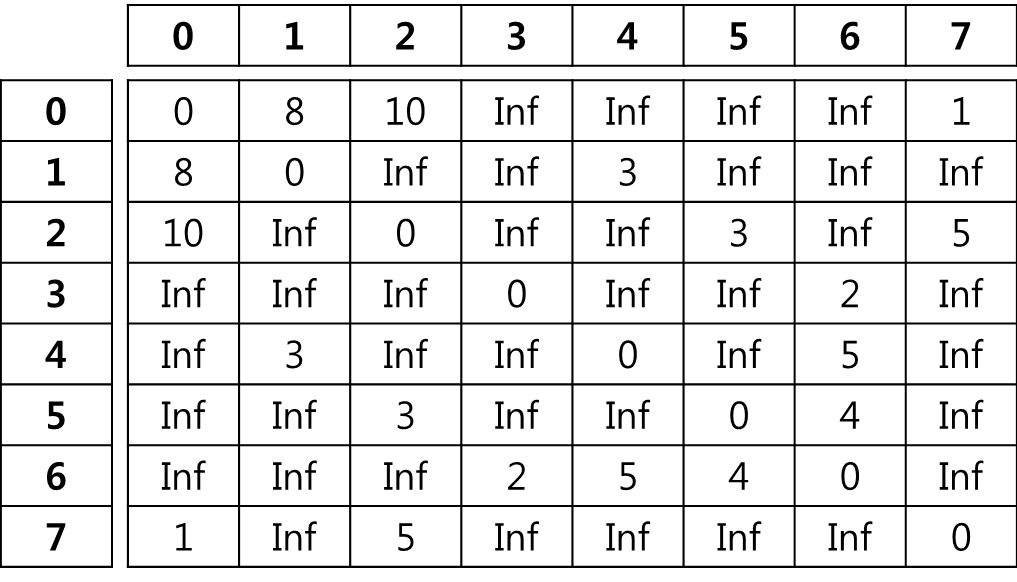
위 그림은 정점에 연결된 Weight를 숫자로 표시한 것인데, 정점간에 연결이 직접연결되어 있을 경우에만 숫자로 표시한다. 다른 정점을 통해서 연결이 되어 있는 정점의 Weight는 일단 Infinity로 나타낸다. 최단 경로는 이 Weight 배열로부터 구할 수 있게 된다. 그럼 주어진 Weight배열을 사용해 정점 0부터 3까지의 최단 경로를 구해보자.

시작은 0번째 정점에서 시작한다. 그리고 0번째 정점은 방문을 한것으로 표시한다. 그 다음 방문할 정점을 선택하는데, 선택하는 방법은 방문하지 않은 정점들중의 0번정점에 연결된 weight 값이 가장 작은 값을 선택한다. 방문하지 않은 정점들중 7번이 가장작으므로 7번을 방문한고, 7번 정점을 방문한 것으로 표시한다.

경로 탐색

0 - 7

7번 정점에 연결된 정점들중, 방문을하지 않은 정점들의 값들을 업데이트 해준다. 7번과 연결된 정점들중 방문하지 않은 정점은 2번뿐이므로 2번만 업데이트 해준다. 업데이트는 작은 값으로 한다. 2번은, 0번과 연결된 weight가 10이었지만, 7번을 거칠 경우 총 weight가 6이 되므로, 6으로 업데이트 해준다.

그리고 다음 방문할 정점을 찾는다. 방문하지 않는 정점들중 weight가 가장 작은 정점은 2번이다.

0 - 7 - 2

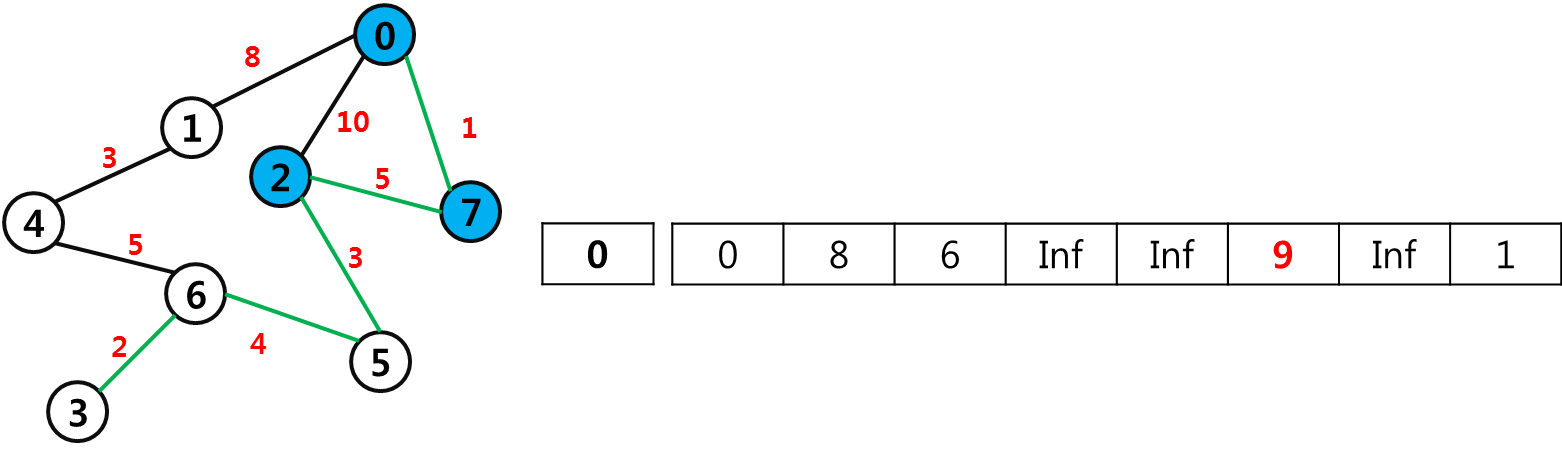
2번과 연결된 정점의 값을 업데이트 해주는데, 2번과 연결된 정점은 5번 뿐이다. 5번 정점은 2번 weight값 6에, 2와 5에 연결된 weight 3을 더해 9로 업데이트 해준다.

그리고 다음 방문할 정점을 찾아 위의 과정을 반복한다. 그러면 아래 그림의 순서대로 진행이 될 것이다.

0 - 7 - 2 - 1

0 - 7 - 2 - 1 - 5

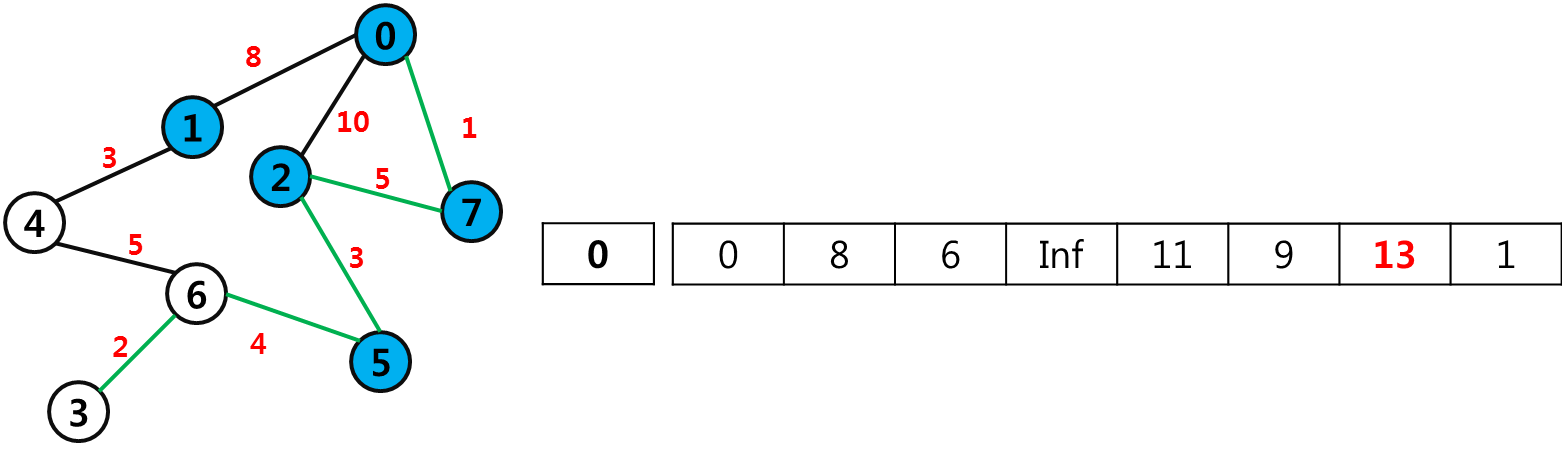
0 - 7 - 2 - 1 - 5 - 4

0 - 7 - 2 - 1 - 5 - 4 - 6

0 - 7 - 2 - 1 - 5 - 4 - 6 - 3

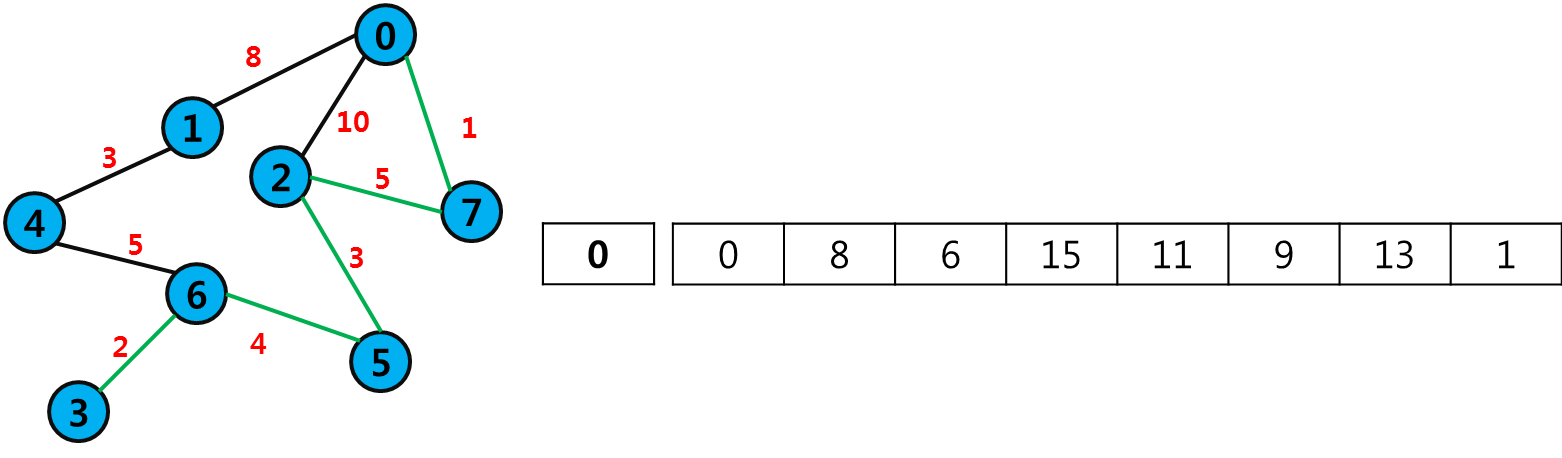
탐색 결과

아래는 모든 정점에 대한 최단 경로를 적용한 결과이다.

All Distance

실제 구현 결과는 아래 코드를 참조한다.

#include <vector>
#include <iostream>
#include <numeric>

using namespace std;

#define Inf    numeric_limits<int>::max()

void addEdge(vector<vector<pair<int, int>>> &graph, int a, int b, int w)
{
    graph[a][b] = make_pair(1, w);
    graph[b][a] = make_pair(1, w);
}

void createWeight(const vector<vector<pair<int, int>>> &graph, vector<vector<int>> &weight)
{
    int size = graph.size();
    for(int i = 0; i < size; i++)
    {
        for(int j = 0; j < size; j++)
        {
            if(i == j)
            {
                weight[i][j] = 0;
            }
            else if(i != j && graph[i][j].second != 0)
            {
                weight[i][j] = graph[i][j].second;
            }
        }
    }
}

int getMinDistance(const vector<int> &minDis, const vector<bool> &visited)
{
    int min = numeric_limits<int>::max();
    int nodeNum = -1;
    for(int i = 0; i < minDis.size(); i++)
    {
        if(visited[i] == false && min > minDis[i])
        {
            min = minDis[i];
            nodeNum = i;
        }
    }

    return nodeNum;
}

void dijkstra(vector<int> &minDis, const vector<vector<int>> &weight, int nodeNum)
{
    int size = minDis.size();

    // 선택된 노드와 각 노드간의 거리를 저장할 배열을 초기화한다.
    // 저장은 선택된 노드와 각 노드간의 Weight값을 사용해 초기화한다.
    vector<bool> visited(size, false);
    for(int i = 0; i < size; i++)
    {
        minDis[i] = weight[nodeNum][i];
    }

    // 현재 선택된 노드를 방문한 상태로 변경한다.
    visited[nodeNum] = true;

    // 현재 선택된 노드를 제외한 나머지 노트를 탐색하기 위해 반복문을 실행한다.
    int index = 0;
    while(index < size - 1)
    {
        // 방문하지 않은 노드중에, 가장 작은 Distance값을 가지고 잇는 노드를 가져온다. (Weight 아님)
        int selectedNode =  getMinDistance(minDis, visited);

        // 가장 작은 Distance 값을 가지고 있는 노드를 방문한다. 이미 방문한적이 있거나, 연결되어있지 않은 노드들은 무시한다.
        visited[selectedNode] = true;

        for(int i = 0; i < size; i++)
        {
            if(visited[i] == false && weight[selectedNode][i] != Inf && weight[selectedNode][i] != 0)
            {
                // 해당노드와의 연결되어 있는 노드들의 Weight값을 얻어와 연결된 노드까지의 Distance를 구한다.
                int newDis = minDis[selectedNode] + weight[selectedNode][i];
                // 가장 작은 Distance로 변경해준다.
                minDis[i] = minDis[i] > newDis ? newDis : minDis[i];
            }
        }
        index++;
    }

    // 각 노드들과의 최단 경로를 출력한다.
    for(int i = 0; i < minDis.size(); i++)
    {
        cout << minDis[i] << " ";
    }
    cout << endl;
}

int main()
{
    int count = 8;

    vector<vector<pair<int, int>>> graph(count, vector<pair<int, int>>(count, make_pair(0, 0)));

    addEdge(graph, 0, 1, 8);
    addEdge(graph, 0, 2, 10);
    addEdge(graph, 0, 7, 1);
    addEdge(graph, 1, 4, 3);
    addEdge(graph, 2, 7, 5);
    addEdge(graph, 2, 5, 3);
    addEdge(graph, 3, 6, 2);
    addEdge(graph, 4, 6, 5);
    addEdge(graph, 5, 6, 4);

    vector<vector<int>> weight(count, vector<int>(count, Inf));
    createWeight(graph, weight);

    vector<int> minDis(count, 0);
    dijkstra(minDis, weight, 0);
    dijkstra(minDis, weight, 1);
    dijkstra(minDis, weight, 2);
    dijkstra(minDis, weight, 3);
    dijkstra(minDis, weight, 4);
    dijkstra(minDis, weight, 5);
    dijkstra(minDis, weight, 6);
    dijkstra(minDis, weight, 7);

    return 0;
}

다익스트라(dijkstra)